 |
SemitotativeGlossary |
Semitotative
Let n ≥ 2 be an integer number base. A semitotative is a necessarily composite, nonregular, and noncoprime number s < n that is the product pq of at least one prime p | n, and at least one prime q that does not divide n. The semitotative does not divide any perfect power of base n, but is not coprime to n. The semitotative is an n-semicoprime number that is smaller than n, thus counted by the semitotative counting function.
The map below plots semitotatives in yellow. Number base n appears on the vertical axis and digit k appears on the horizontal.
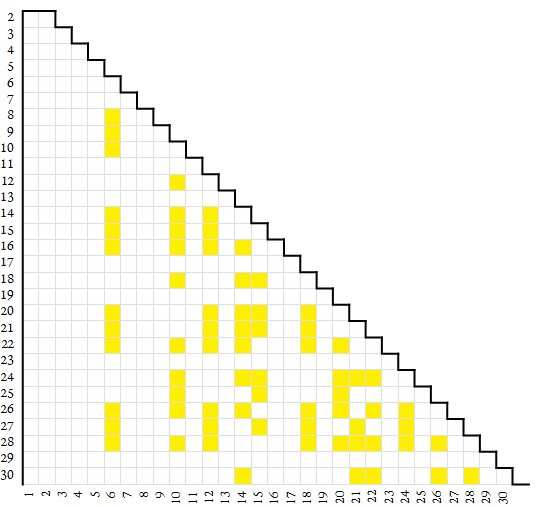
The semitotative as a product of regular and coprime factors
Since the semitotative is a kind of composite number that is the product of at least one divisor and one nondivisor prime, we may express all semitotatives as a product of a regular factor r and coprime factor t:
s = r × t.
Therefore, the semitotative inherits richness ε from r and period λ from t. Hence, as denominators in a unit fraction 1/s, when expanded in base n, we see ε nonrepeating digits followed by a recurrent set of λ digits. Example: the decimal semitotative 6, as a unit fraction and decimally expanded, exhibits one non-recurrent digit after the decimal point followed by a recurrent 6, .1666…, since we can write 6 = 2 × 3, where 2 is a divisor of 10 and 3 is coprime, but divides 10 − 1 = 9, enjoying a period of 1. For decimal 1/14, 14 = 2 × 7; 2 is a divisor with richness 1, and 7 a decimal long prime with period 6, we have 1/14 = .0714285714285…, the 0 never repeated, the “714285” repeated endlessly.
The reckoning of n-semicoprimes s as the product of regular and coprime factors is useful in examination of their behavior in base n. This is because regular richness ε inherited from regular r and period λ inherited from coprime t govern which divisibility tests pertain to s in base n. The mixed-recurrent base-n expansion of 1/s is likewise explained by its regular and coprime factors.
A kind of neutral number
The semitotative s = ξt is one of two kinds of neutral numbers ξ with respect to base n; i.e., these are nondivisors that are also not coprime to n, and thus are not counted by the divisor counting function τ(n) and the Euler totient function φ(n).
The semitotative counting function
The semitotative counting function ξt(n) = A243823(n) is the number of semicoprime s < n:
ξt(n) = n − (RCF(n) + φ(n) − 1),
= ξ(n) − ξd(n)
or in terms of the OEIS:
A243823(n) = n − (A010846(n) + A000010(n) − 1),
= A045763(n) − A243822(n)
For prime p, ξt(p) = 0. In other words, prime bases p do not have semicoprimes smaller than p (i.e, semitotatives).
For prime powers pm > 4, semitotatives are the only pm-neutral numbers k < pm. We note that since n = 4 is the smallest composite and since semitotatives must be composite and less than n, n = 4 cannot have semitotatives.
The number n = 6 is the only n with ξd > 0 but ξt = 0. That is, with a semidivisor less than n (i.e., 4) but no semitotative. We observe that for n = 6, we can produce a semicoprime pq = 10 with the least prime divisor p = 2 and least prime nondivisor q = 5; since the number of q is infinite, and since we may use any number of p (but at least 1) and any number of q (but at least 1), we can produce an infinite number of 6-semicoprime numbers, but none less than 6.
All other composite n have at least one semitotative ξt < n, since we can produce ξt = pq with pq < n from the least prime divisor p and the least prime nondivisor q.
Behavior of semitotatives in base n
- Fractions expanded in base n with a semitotative ξt = r × t as the denominator are mixed recurrent, involving a number ε of nonrepeating digits followed by a repeating sequence of λ digits, where ε is the richness of the regular factor r and λ is the period of the coprime factor t. Example, decimal 1/12 = .08333… (12 = 4 × 3, where 4 has richness 2 and 3 has period 1), while octal 1/6 = .1252525… (6 = 2 × 3, where 2 has richness 1 and 3 has period 2 in base 8).
- Semitotatives ξt have periods in the multiplication table that are briefer than ξt.
- Base-n divisibility tests that pertain to semitotatives ξt = r × t are compound, regarding the regular divisibility test for r, and some coprime neighbor test. Unless the richness of is low and the coprime has the briefest periods of 1 or 2, the compound divisibility test may prove impractical. An example of a practical compound divisibility rule pertaining to a semitotative is that for decimal 6. An arbitrary number x is divisible by 6 if x is even and if the sum of digits of x is divisible by 3.
- A semitotative is said to be “opaque” if there are no practical intuitive divisibility tests that apply to it. In base ten, the semitotative 6 is transparent, but the duodecimal semitotative ten is opaque since 5 is a duodecimal long prime. We may ameliorate some opaque semitotatives
- The minimum case of semitotative ξt is digit 6 base 8. Note that all bases n have semicoprimes s > n. We can produce an n-semicoprime s by multiplying n by any number t such that gcd(t, n) = 1.
Inheritance of regular and coprime properties by semitotatives
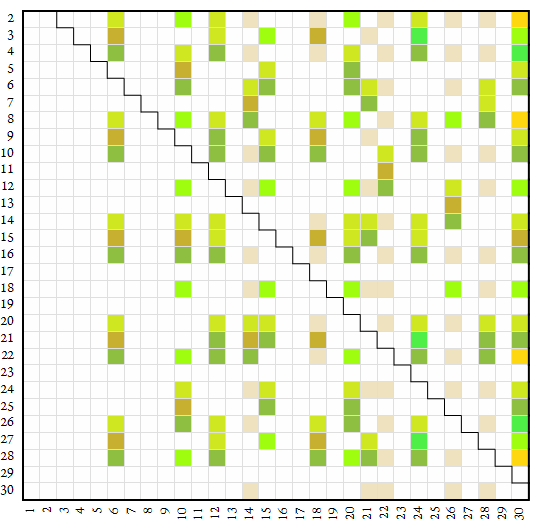
There are many “flavors” of semicoprimes (of which, semicoprimes less than n are semitotatives), principally governed by the properties of the coprime factor. The regular factor’s richness ε governs the practicality of any regular inheritors. Generally, if ε > 2, then a regular inheritor normally proves impractical. Here is a list of some of the many flavors of semicoprimes:
- Alpha inheritor (sα ■) — a necessarily composite s = r × tα semicoprime to n such that tα | (n + 1) and r is practical. In decimal, the number 22 is an alpha inheritor since 22 = 2 × 11; the decimal evenness test is practical, and 11 = (10 + 1). Therefore we have a workable compound divisibility test for 22 in base 10: if x is even and divisible by 11, then x is divisible by 22. The decimal number 176 is not a practical alpha inheritor.
- Omega inheritor (sω ■) — a necessarily composite s = r × tω semicoprime to n such that tω | (n − 1) and r is practical. In decimal, the number 6 is an omega inheritor since 6 = 2 × 3; the decimal evenness test is practical, and 3 is a divisor of (10 − 1). Therefore we have a workable compound divisibility test for 6 in base 10: if x is even and divisible by 3, then x is divisible by 6. The decimal number 48 is not a practical omega inheritor. The omega inheritor is perhaps the most user-friendly flavor of semitotative, especially when the regular factor is a divisor of the base. Decimal 6 is an example of the very most friendly flavor of semitotative possible.
- Alpha omega inheritor (sαω ■) — a necessarily composite k = r × tα × tω semicoprime to n such that tα | (n + 1) and tω | (n − 1) and r is practical. In base 34, the number 30 is an alpha omega inheritor, since 30 = 2 × 3 × 5; 3 | 33, 2 | 34, and 5 | 35. Therefore we have a practical three-part compound divisibility test for 30 in base 34: if x is even and divisible by 3 and 5, then x is divisible by 30. In an odd base n, we interpret the coprime factor 2 as 2 | (n − 1) since the digit sum divisibility test is simpler. Therefore any even semicoprime also divisible by a practical regular r and a factor tα | (n + 1) is deemed an alpha omega inheritor. In pentadecimal (base 21), 66 is an alpha omega inheritor since 2 | 20, 3 | 21, and 11 | 22.
- Alpha-2 inheritor (sα2 ■) — a necessarily composite s = r × tα2 semicoprime to n such that tα2 divides (n² − 1) but neither (n + 1) nor (n − 1) and r is practical. In base 12, the number ten is an alpha-2 inheritor, since 10 = 2 × 5 and though 2 | 12, 5 | (12² + 1) but neither 11 nor 13. Since 2 is a divisor of 12, the rule is practical and would likely serve as a major and relatively often-used method in a duodecimal civilization, akin but not precisely analogous to the decimal Rules of 3 and 9. Likewise, ten is an alpha-2 inheritor in octal and it would also be expected that the useful rule of 5 would subtend in an octal culture.
- Omega-2 inheritor (sω2 ■) — a necessarily composite s = r × tω2 semicoprime to n such that tω2 divides (n² + 1) and r is practical. The omega-2 inheritor is relatively obscure, since most of the smaller divisors of omega-2 pertain to the above-mentioned alpha or omega. In base 27, the number 8 is an omega-2 totative (8 | 27² − 1). Therefore, the number 24 is an omega-2 semitotative with regular factor 3 (a divisor with richness 1) and 8 as the coprime factor. The omega-2 test in base 27 perhaps might prove somewhat useful.
- Opaque semitotative (■) — a semitotative s = r × t wherein r is impractical or t does not divide (n² − 1). Strictly speaking, opacity had applied to any practical semitotative where the coprime factor t divides (n − 1) or (n + 1).
The map below plots the flavors of semitotatives. Number base n appears on the vertical axis and digit k appears on the horizontal.
On the utility of bounding n-semicoprimes by n
Because n-semicoprime numbers are neither coprime to n nor n-regular, the distinction of the semitotative as a semicoprime less than n proves perhaps more “artificial” than the distinction of semidivisors less than n, or totatives of n, which are n-coprime numbers less than n. This is because naffects no limit upon n-semicoprime numbers, whereas the totatives of n are reduced residues that can be used mod n to determine any n-coprime number, and semidivisors are a type of n-regular number along with divisors of n; no divisor can exceed n itself, thus all n-regular numbers larger than n are semidivisors.
The semitotative is so-named as, among “digits” 0 ≤ k < n (the digit 0 taken to signify congruence with n and not actual zero), as regards the human use of number bases, semitotatives generally behave as resistance like the totatives. Further, the semitotative is a product involving at least one factor coprime to n.
Semitotatives in the OEIS
There are a few sequences in the OEIS that examine the semidivisors 1 < ξd < n:
A243823: Semitotative counting function.*
A272619: Semitotatives of n.*
A304572: Characteristic function of numbers m such that m divides no integer power of n yet gcd(m, n) > 1.*
A292867: A243823 recordsetters.*
A293868: Records in A243823.*
A096014: Smallest m semicoprime to n: product of least prime factor p and smallest prime q that does not divide n.
A291989: Least m > n semicoprime to n.* (i.e., the smallest semicoprime not a semitotative.)
A300858: A243823(n) − A243822(n). (A300858(p) for p prime = 0, for n = {6, 10, 12, 18, 30}, A300858(n) is negative.)
A300860: A300858 recordsetters.*
A300861: Records in A300858.*
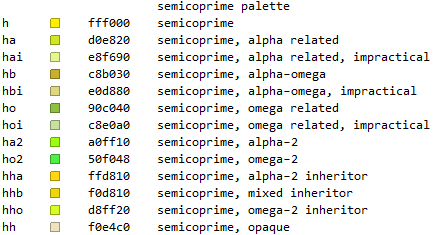
Color Canon
The colors used to represent semitotatives in this work appear in the table below:
Provenance of the term “semitotative”
The term “semitotative” is a 2008 coinage of the author of this work. The term applied to one of two species of n-neutral number which was not a composite product restricted to primes p | n. Seeing primes, with regard to n, as either a divisor p or a nondivisor (and thereby coprime) q, the semi-totative is the product of at least one p and at least one q and are always composite. In researching an extant name for such an entity, the author turned up no standard. The term settled mainly through euphony with the term for the other n-neutral entity, the semidivisor, as the two terms for the species influenced one another. Later consideration saw the term “semidivisor” expand to any nondivisor n-regular, while the term “semicoprime” developed to cover any product of n-regular r and n-coprime t. The “totative” component of the word implies that we refer to entities k ≤ n, therefore a new term became necessary to refer to any product as defined above, unbounded by n.
The term attempts to succinctly describe a composite integer k that is the product of a regular number r and a totative 1 < t < n, whereas “semicoprime” refers to a composite integer k that is the product of a regular number r and any number t > 1 coprime to n.
References
Michael De Vlieger, Exploring Number Bases as Tools, ACM Inroads, 2012, Vol. 3, No. 1, 4-12.
Hardy & Wright, 141-145.