 |
Omega-2 FactorGlossary |
Omega-2 (ω2) Factor
Consider the number base n. An omega-2 factor tω2 is an integer necessarily coprime to n that divides ω2 = (n² − 1) but neither (n − 1) nor (n + 1) (recognizing that factors of these algebraic factors have simpler divisibility tests). In base n, ω2 = (n² − 1) is always written as a pair of the base's largest digits, e.g., decimal 99 or octal “77”, assuming standard positional notation. In the decimal case, 99 and 33 are omega-2 factors, but 11, 9, and 3 are alpha (for the first) and omega (for the latter 2).
In base n, the omega-2 factor tω2 enjoys special properties that can facilitate work with these numbers.
The map below plots omega-2 factors in light blue and semicoprime omega-2 inheritors in green. Number base n appears on the vertical axis and digit k appears on the horizontal.
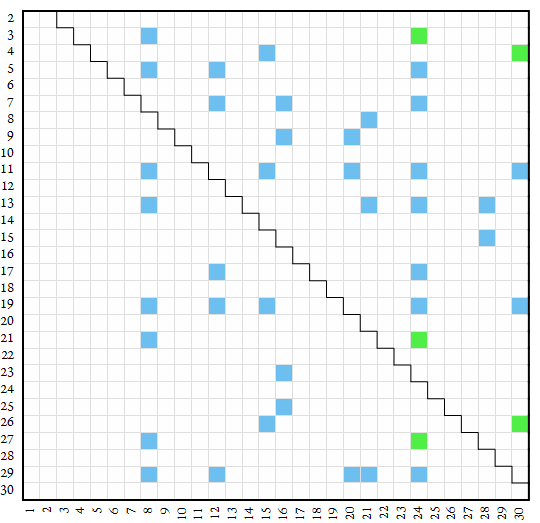
Divisibility test for omega-2 factors
The base-n divisibility test applying to an omega-2 factor, involving the pairing of base-n digits beginning with the unit digit and working towards significance (meaning leftward from the radix point), then taking the digit sum of the numbers formed by these digit pairs.
This divisibility test is relatively obscure, since many of the most useful factors of (n² − 1) are indeed divisors of its algebraic factors (n − 1) or (n + 1). In decimal, the omega-2 divisibility test applies to 33, but most might be inclined instead to test for 3 and use the already-obscure rule of 11, rendering a compound test.
We can use undecimal (base 11) to examine the divisibility rule that applies to omega-2 factors. In base 11, the number 8 is an omega-2 totative. The undecimal number “3094” is divisible by 8 since “30” + “94” = “114”, and “01” + “14” = “15”, which is 1 eleven and 5 (i.e., decimal 16), which is clearly divisible by 8. We note undecimal “3094” is the fourth power of 8 (decimal 4096).
The omega-2 rules apply to 8 in bases that are congruent to ±3 (mod 8). Quinary (base 5) sees 8 as an omega-2 totative. Regarding the number 12, the omega-2 rules apply in bases n ≡ 5 (mod 12), therefore bases 5 and 7 test for divisibility by 12 using omega-2.
In base 21, the number 8 is an omega-2 totative that conveys omega-2 divisibility tests to 24 and 56 (among other products with unvigesimal-regular numbers).
Numbers k that are omega-2 for some base n
Generally, it appears that numbers k that do not have a primitive root (OEIS A033949, see comments) occur as omega-2 for some base n.
Omega-2 inheritors
An omega-2 inheritor is a necessarily composite sω2= r × tω2 semicoprime to n such that the coprime factor tω2 divides (n² − 1) but neither (n − 1) nor (n + 1), and the regular factor r is practical. Armed with a regular divisibility test for r and an omega-2 divisibility test for tω2, we can use a compound divisibility test for the omega-2 inheritor sω2. In base 21, given the above-mentioned test for 8 and the unvigesimal regular test for three (i.e., any unvigesimal number ending in digits {0, 3, 6, 9, 12, 15, 18}), we can determine whether an arbitrary unvigesimal number x is divisible by “13” (decimal 24). Example: the unvigesimal number “169” is evidently divisible by 3 since it ends in digit 9; we know it is also divisible by twenty-four since “01” + “69” = “6a” (where “a” = digit ten), and 6 twenty-ones and ten (decimal 136) is divisible by 8. This is akin to the decimal divisibility test for 6; we know if a number is divisible by three and is even, it is divisible also by 6.
The omega-2 inheritors appear to be rather sparse, but if we pan out to show bases up to 60, more of these become evident. We note that 24 is an omega-2 inheritor in bases 21, 45, and 51; 30 is same for bases 34 and 56; 42 is an omega-2 inheritor in base 50, and 48 is an omega-2 inheritor in base 57. Base 45 has two omega-2 inheritors among its digits (24 and 40). Small bases also possess omega-2 inheritors: decimal 12 and 40 in base 5, decimal 12 in base 7, decimal 88 in base 11, ,
Such divisibility tests certainly may prove rather ineffective for human use, at least from the standpoint of a native, decimal culture, since they tend to apply to relatively large numbers. The quinary and septenary divisibility tests for 12 are perhaps more practical and necessary given that 5 and 7 are prime.
Color Canon
The colors used to represent omega-2 factors in this work only appear in enhanced maps. In such maps, the omega color code is enhanced, and the omega-2 takes on the unaccentuated omega color.
![]()