 |
SemidivisorGlossary |
Semidivisor
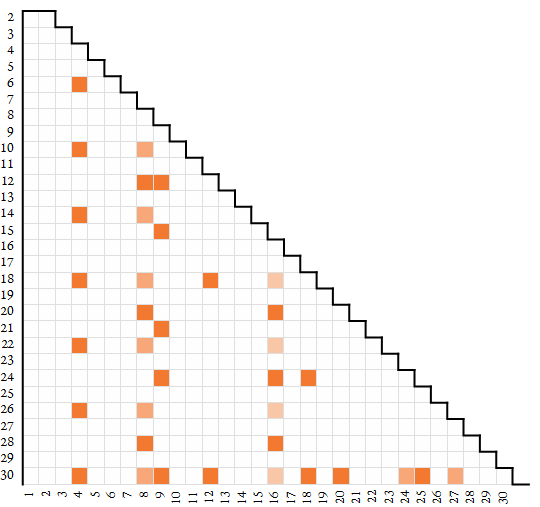
Let n ≥ 2 be an integer number base. A semidivisor is a necessarily composite n-regular number r | nε with richness ε > 1. Primes p and prime powers pm have semidivisors that exceed the base and are also perfect powers pk with k > m. All composite numbers n have at least one semidivisor r < n. The smallest case of semidivisor is r = 4, n = 6. Almost all n-regular numbers r for n > 1 are semidivisors.
The map below plots semidivisors in shades of orange; the shade is lighter for increasingly impractical semidivisors. Number base n appears on the vertical axis and digit k appears on the horizontal.
A kind of neutral number
The semidivisor r = ξd is one of two kinds of neutral numbers ξ with respect to base n; i.e., these are nondivisors that are also not coprime to n, and thus are not counted by the divisor counting function τ(n) and the Euler totient function φ(n).
A kind of regular number
The divisor d is a special case of n-regular number such that d | n ε with 0 ≤ ε ≤ 1, with d = 1 the only divisor that divides n0. A semidivisor is simply a nondivisor regular number r | n ε with ε > 1.
Therefore, the semidivisor r is both regular and neutral to n.
The semidivisor counting function
The semidivisor counting function ξd(n) = A243822(n) is the number of semidivisors ξd < n:
ξd(n) = RCF(n) – τ(n),
= ξ(n) − ξt(n)
or in terms of the OEIS:
A243822(n) = A010846(n) − A000005(n),
= A045763(n) − A243823(n)
For prime p, ξd(p) = 0. In other words, prime bases p do not have semidivisors smaller than p.
For prime powers pm, ξd(pm)= 0. All semidivisors of prime power bases are larger than the base.
Furthermore, these semidivisors are powers pk with k > m.
All composite n that are not prime powers have at least one semidivisor ξd < n.
The number n = 6 is the only n with ξd > 0 but ξt = 0. That is, with a semidivisor less than n (i.e., 4) but no semitotative.
Behavior of semidivisors in base n
- Fractions expanded in base n with a semidivisor ξd as the denominator terminate after more than 1 digit, e.g., decimal ¼ = .25, while duodecimal ¼ = .3.
- Semidivisors have a multiplicative complement g′ such that nε = ξd · g′.
- Semidivisors have periods in the multiplication table λ = GCD(n, ξd), and unit cycles κ that are terminating rational numbers. The periods and cycles are not equal (λ ≠ κ).
- Unit fractions 1/ξd expanded in base n involve ε places after the radix point, with the base-n representation of g′at the n −ε place.
- We can test for divisibility of an arbitrary nonzero integer x by sd in base r by examining ρ least significant digits: if this value matches one of the g′ multiples of ξd ≤ nε (with place value “0” signifying x ≡ 0 (mod r)) then x is divisible by ξd.
- Base-n divisibility tests that pertain to semidivisors involve examining two or more final digits.
- Only semidivisors with low richnesses may prove practical to use in base n.
- Any composite number can have a compound divisibility rule involving all the divisibility tests of each distinct prime power p μ of ξd. At times it may be easier to rely on these compound regular divisibility tests than the regular IDT.
- The minimum case of semidivisor ξd is digit 4 base 6. Note that all integer bases n have semidivisors ξd > n. Any perfect power of n is a semidivisor.
Semidivisors in the OEIS
There are a few sequences in the OEIS that examine the semidivisors 1 < ξd < n:
A243822: The semidivisor counting function ξd(n) = the number of semidivisors ξd < n.
A272618: Row n of this sequence lists semidivisors ξd < n.
A293555: Numbers n that set records for the semidivisor counting function ξd(n).
A295523: Numbers n that have more semidivisors than semitotatives (the two kinds of n-neutral number).
A299991: Numbers n that have more semidivisors than divisors (two kinds of n-regular number).
A299992: Numbers n that have fewer semidivisors than divisors.
A300155: Numbers n that have equal numbers of semidivisors and divisors.
A300156: Numbers n that set records for the difference between the semidivisor counting function ξd(n) and the divisor counting function τ(n).
A289280: Smallest n-regular r > n (the smallest semidivisor r greater than n).
Color Canon
The colors used to represent semidivisors in this work appear in the table below:
Provenance of the term “semidivisor”
The term “semidivisor” is a 2008 coinage of the author of this work. The term applied to one of two species of n-neutral number which was a composite product restricted to primes p | n. In researching an extant name for such an entity, the author turned up no standard. The term “quasi-divisor” was also considered, but semidivisor became favored mainly through euphony with the term for the other n-neutral entity, the semitotative (or semicoprime), as the two terms for the species influenced one another.
The term attempts to succinctly describe an integer k that “closely approaches” dividing n, instead dividing some perfect power of n.
References
Michael De Vlieger, Exploring Number Bases as Tools, ACM Inroads, 2012, Vol. 3, No. 1, 4-12.