 |
Making Hexadecimal UsefulRadicologist Essays |
Can we render hexadecimal plausibly useful?
Since the advent of the personal computer and before the ubiquity of the internet connection, intelligent dreamers would lie back with time to kill, maybe in boring algebra classes or on long bus rides, and ponder which number base is best.
What do we mean by “best”? The brilliant teenager might ponder this; he usually meant “most useful”, which would include simplifying arithmetic and making more fractions “come out”. She could also consider other items, like making it easy to pick out squares etc., but usually these two major goals constituted what was meant by “best”. Implicitly, “best” pertained to human use.
Given the computer and knowing about code and memory addresses, many in the 70s, 80s, and 90s (possibly into the 2000s up to the ubiquity of smartphones) this dreamer would seize on the fact that hexadecimal “is used by computers”, and decide that this would be the solution for a modern world. Dream over—for now.
When the kid returns to the tantalizing thought on another boring trek, maybe waiting for Mom or Dad to drive up and take the kid home, the dream continues.
The world would use hexadecimal and all would be made better, merely by dint of rhyming with our machinery. We have feet that fit into the technology we call shoes, and we don’t usually smash our feet to fit them, but somehow this does not come across mind. We follow our line of reasoning perhaps without questioning how the base is used in computers.
Hexadecimal poses several obstacles that decimal and smaller bases might not. We are dissatisfied with decimal. We don’t like its fractions or maybe the fiveyness of it all; we are most interested in doubling and halving because that’s easy to understand. Decimal of course is even and that is good. Why not make it even-even? Or even-even-even—or go for broke and make it quadruply even? That would give us a larger base that makes numbers seem more compact. We need six new numerals; in computers they use the alphabet’s first six letters (this was not ubiquitous at the start, and computers also sometimes used octal for addresses). Satisfied with that, we might proceed to further thought.
Some are dissatisfied with letters as numerals; they can get confused and they can get hammered into cynical “leetspeak”: deadbeef and cafebabe (deadbeef and cafebabe) signifying the decimal numbers 3,735,928,559 and 3,405,691,582, etc. We could make new hexadecimal numerals; others have created proposals for such. Since we’re dreaming we could create whatever we like and use them as numerals, or just append the first six letters, capital or lowercase, and dispense with the art exercise.
The mechanics of base sixteen have been described elsewhere in this forum; we won’t show pretty charts and such in this thread, but will instead proceed to describe how the base behaves especially compared to decimal.
The first thing we might try is making a hexadecimal multiplication table. It’s quite a bit larger; a 256-square table in place of the familiar decimal 100-square (or 12× 144-square table), but there are 136 vs. 55 (or 78) products in the table. If we are avid we might attempt to memorize the table. We’re older than we were when we learned to multiply, so it should go faster. We might notice that the smaller decimal table had the 5× line that was mighty easy to memorize: 5, 10, 15, 20, etc., and that is now the 8× line hexadecimally. In the hexadecimal table the 4× line is also pretty simple (4, 8, c, 10, 14, 18, 1c, 20, …). The fun 9× line in the decimal table resembles the f× line in the hexadecimal. We might notice the hexadecimal table is fairly large and also that there are pretty rough lines to memorize, like the larger odd digits outside of f. Daunting.
Addition might be a brute force memorization situation.
Many of the fractions we use most seem simpler than in decimal: 1/2 = .8, 1/4 = .4, 3/4 = .c, and the odd eighths are .2, .6, .a, and .e, respectively. The thirds are as they appear decimally, except we repeat 5 and its double, a, instead of 3 and 6: 1/3 = .555…, and 2/3 = .aaa…. Fifths are not as simple: 1/5 = .333…, and sevenths are perhaps easier: 1/7 = .249249…. Some fractions are ugly, but perhaps we don’t need them that often.
We have a lot of keen divisibility tests hexadecimally. Of course, we know a number is even if it ends in an even digit, and divisible by 4 if it ends in (0, 4, 8, c), by 8 if it ends in 0 or 8. We also know if a number is divisible by 3, 5, or f if the sum of the number’s digits is likewise divisible by that respective number. By extension we have nice composite tests for 6, a, and c. The numbers we have no intuitive tests for are 7, 9, b, d, and e.
We might one day compare hexadecimal to other bases and could conclude that other bases might pose advantages or we might remain steeped in our conviction that hex is best. Some of the arguments for other bases or even retaining decimal is more advantageous than going hex. Examples we might come across are the “simpler fractions” of base 12 (1/2 = .6, 1/4 = .3, 3/4 = .9, 1/3 = .4, 2/3 = .8) and its pattern-rich multiplication table (3: 3, 6, 9, 10, 13, 16, …; 4: 4, 8, 10, 14, 18, …) and the fact it is divisible by 2, 3, and 4. Decimal is divisible by 5 and so more fractions terminate decimally. Both these bases are smaller than sixteen and are perhaps more convenient and efficient.
One thing that could have happened early in the development of a hexadecimal culture is the adoption of “bitwise” numerals and the retention of “mediation/duplation”.
A bitwise numeral is one that graphically demonstrates the bits that equate to the numeral. For instance, the numeral 3 = “0011” in binary. So the numeral 3 should somehow show these four bits. In 1968, Bruce Martin described hexadecimal numerals that bundled bits. I like to use this proposal because the “bitwise” idea is perhaps most clear in Martin’s arrangement. A recent proposal can be found in the 2017 Cumings-Vitolins paper that might have as much merit as the dozens before and similar to it, but Martin’s proposal seems more basic and primitive, thereby superior (Mies van der Rohe: “less is more!”). Below we have the argam numerals, the traditional alphanumeric numerals, and Bruce Martin's hexadecimal numerals. (The term bitwise is an adjective I append to the sort of numerals Martin’s are, that is, numerals that display their bit values).

Another view of Bruce Martin’s numerals:
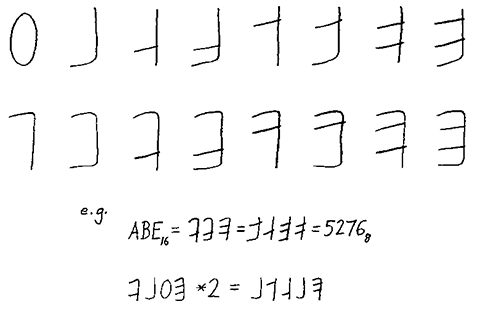
Bitwise numerals could facilitate hexadecimal operations. To add bits in the digit, we merely place a stroke to add 0 + 1, clear the rank and increment the next rank if we add 1 + 1, or do nothing to add 0 + 0. For multiplication/addition, we instead use “mediation/duplation” or halving and doubling. (This algorithm is called “Russian multiplication” by some.)
In hexadecimal it would be conceivable we would learn the roll table, so-named for the “roll” operation on some calculators:
| 1 | 2 | 4 | 8 |
| 3 | 6 | c | 18 |
| 5 | a | 14 | 28 |
| 7 | e | 1c | 38 |
| 9 | 12 | 24 | 48 |
| b | 16 | 2c | 58 |
| d | 1a | 34 | 68 |
| f | 1e | 3c | 78 |
(in Martin’s “bitwise” notation:)
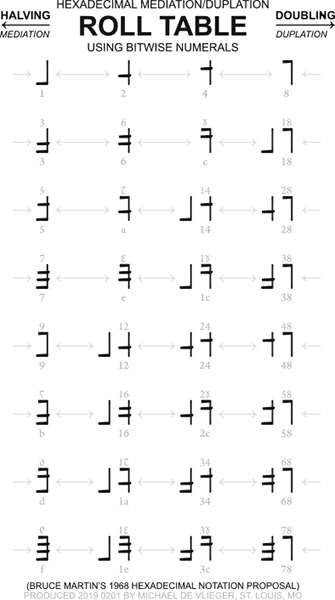
(Download a business-card sized version of the roll table in Martin's notation here)
It seems plain that stating the roll table per Martin’s numerals is plainer and more logical than trying to use numerals like the ones we use in decimal. To double or roll up a Martin numeral, we merely move its bits up. Thus, 7 = 7 or in binary 0111. Let’s double the bits: 0111, 1110, 0001 1100, 0011 1000. This translates to 7, e, 1c, 38, and it seems clear all we have with Martin’s numerals is a grouped and upturned notation for bits. We can see all we are doing is shifting the bits to the next rank. Doubling and halving are facilitated by clear bitwise digits.
We can “roll” decimally; all a roll consists of is doubling (for rolling up) or halving (rolling down). Therefore, when we roll the decimal number 12, we get 24, 48, 96, 192, 384, 768, etc. Rolling down we get 6, 3 (and non-integers thereafter). This seems messy in decimal, but in hexadecimal it has a periodic pattern: decimal 12 = hexadecimal c: 18, 30, 60, c0, 180, 300, 600, c00, etc. From this we can see that all the numbers in this sequence pertain to a line, putting the smallest odd number first, 3 → 6 → c → 18. This is one entry in the hexadecimal roll table. Suppose we have a number like hexadecimal 65, that is not on a roll table line. We can roll the numbers and add them in their place: 65, ca, 180 + 14, 300 + 28, 600 + 50 = 650, etc., thus, 65, ca, 194, 328, etc.
We can multiply two numbers using this method. If we have an odd multiplier (i.e., the first of the two numbers to multiply) we flag the multiplicand (the second number) to be added to derive the answer. At each step we halve the multiplier (discarding remainders) and double the multiplicand. Here is an example:
Multiply hexadecimal 7c × 219:
7c × 219
3e × 432
1f × 864 → 864
f × 10c8 → 10c8
7 × 2190 → 2190
3 × 4320 → 4320
1 × 8640 → 8640
Adding all the numbers on the right, we have: 1041c.In hexadecimal with bitwise numbers this is even easier, as we can dispense with the multiplier, convert it to bits, and merely double the multiplicand, taking only those terms that correspond with the “1” bits:
7c × 219 = 7c × 219. Reading the bits of the multiplier, we have 1111100. We reverse this string and need to roll up the multiplicand 7 times: 219, 432, 864, 10c8, 2190, 4320, 8640. Now it’s clear that we can ignore the first two terms (since the last two bits are zeros) and add the remaining five to get 1041c.
Multiply hexadecimal 7c × 219:
(219)
(432)
864
10c8
2190
4320
+ 8640
1041c
Perhaps one skilled in this process is adept enough to skip the zero steps and roll up twice or thrice without writing numbers, making this process more efficient.
Essentially Martin’s notation is merely the partitioning of a binary number into “nybbles” of four bits each:
1041c = 0001 0000 0100 0001 1100, or perhaps visually simpler:
1041c = −−−1 −−−− −1−− −−−1 11−−.
Hexadecimal performed this way is perhaps akin to binary, and could proceed rather quickly.
Is hexadecimal a workable solution for human computation? Though it seems alien to the way we do our arithmetic, it seems simple enough to learn such that it could serve as a base that facilitates everyday human computation.
Written Tuesday 5 February 2019 by Michael Thomas De Vlieger.