 |
Alpha NumberGlossary |
The alpha number (n + 1) and its factors
Regarding the number base n, the alpha number is simply (n + 1). The factors tα > 2 of (n + 1) are called alpha factors in this work. These factors are integers necessarily coprime to n, but have the brief semiminimum period 2. In base n, α = (n + 1) is always written “11”, assuming standard positional notation and Hindu-Arabic-like numerals.
The alpha number tα is a handy concept regarding number bases since the number and its factors have a relatively simple and intuitive divisibility test and a mixed recurrent expansion of 1/tα involving 2 recurrent digits. These traits are inherited by products of tα and n-regular numbers r.
The map below plots alpha factors in green (tα ■). Number base n appears on the vertical axis and digit k appears on the horizontal. The number 2 in odd bases (tαω ■) is also technically a factor of (n + 1) but is also same of omega = (n − 1). Since the omega divisibility rule is simpler, we usually consider 2 in an odd base an omega factor.
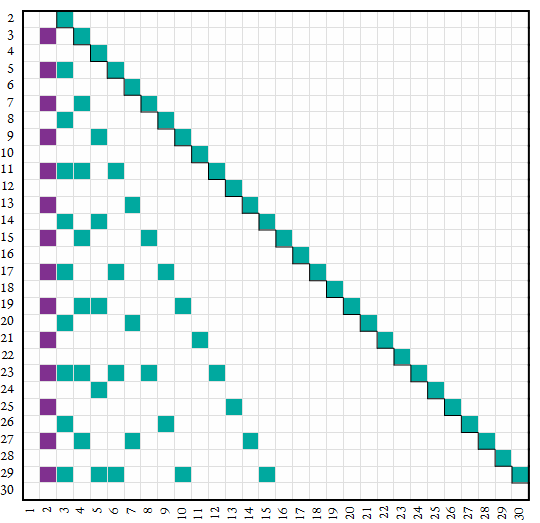
The alpha number in the multiplication table of base n
In any base n, α is written “11” and its small multiples kα with 1 ≤ k ≤ (n − 1) are a pair of the same digit. The pattern is distinctive and easy to memorize. The square of alpha for bases n > 2 is always written “121”, while the cube is always “1331” for bases greater than 3. For example, the decimal 11 × facts are:
11 22 33 44 55 66 77 88 99 110 121 …
In base 8, octal “11” is the square of 3, thus we see every third multiple of three is a pair of the same digit.
3 6 11 14 17 22 25 30 33 …
The alpha number and its factors as denominators, expanded in base n
Alpha (n + 1) is coprime to n, since the smallest prime is 2; no prime factor can be found that divides both n and (n + 1). Alpha factors tα > 2 in the denominator 1/tα have a 2-digit purely recurrent expansion in base n, as the recurrent period of 1/tα is 2. In decimal, 1/11 = .090909…. In octal, 9 is alpha and is written “11”; “1/11” = .070707… and 1/3 = .252525….
The table below diagrams the behavior of numbers k at the top as unit fractions 1/k, with bold numerals nonrepeating, italic repeating. The alpha numbers and their factors tα > 2 appear in green (■). Examples: we observe that in base 9, 1/5 = .171717…, in base 14, 1/3 = .494949…, and in base 19, 1/4 = .4e4e4e…. If we move up to the next base (n + 1), we have regular fractions; in base 9 +1, 1/5 = .2, in base 14 + 1, 1/3 = .5, and in base 19 + 1, 1/4 = .5.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 2 | 1 | 01 | 01 | 0011 | 001 | 001 | 001 | 000111 | 00011 | 0001011101 | 0001 | 000100111011 | 0001 | 0001 | 0001 |
| 3 | 1 | 1 | 02 | 0121 | 01 | 010212 | 01 | 01 | 0022 | 00211 | 002 | 002 | 001221 | 00121 | 0012 |
| 4 | 2 | 1 | 1 | 03 | 02 | 021 | 02 | 013 | 012 | 01131 | 01 | 010323 | 0102 | 01 | 01 |
| 5 | 2 | 13 | 1 | 1 | 04 | 032412 | 03 | 023421 | 02 | 02114 | 02 | 0143 | 013431 | 013 | 0124 |
| 6 | 3 | 2 | 13 | 1 | 1 | 05 | 043 | 04 | 03 | 0313452421 | 03 | 024340531215 | 023 | 02 | 0213 |
| 7 | 3 | 2 | 15 | 1254 | 1 | 1 | 06 | 053 | 0462 | 0431162355 | 04 | 035245631421 | 03 | 0316 | 03 |
| 8 | 4 | 25 | 2 | 1463 | 125 | 1 | 1 | 07 | 06314 | 0564272135 | 052 | 0473 | 04 | 0421 | 02 |
| 9 | 4 | 3 | 4 | 17 | 14 | 125 | 1 | 1 | 08 | 07324 | 06 | 062 | 057 | 053 | 05 |
| 10 | 5 | 3 | 25 | 2 | 16 | 142857 | 125 | 1 | 1 | 09 | 083 | 076923 | 0714285 | 06 | 0625 |
| 11 | 5 | 37 | 28 | 2 | 19 | 163 | 14 | 124986 | 1 | 1 | 0a | 093425a17685 | 087 | 08 | 0762 |
| 12 | 6 | 4 | 3 | 2497 | 2 | 186a35 | 16 | 14 | 12497 | 1 | 1 | 0b | 0a35186 | 09724 | 09 |
| 13 | 6 | 4 | 3 | 27a5 | 2 | 1b | 18 | 15a | 13b9 | 12495ba837 | 1 | 1 | 0c | 0b36 | 0a74 |
| 14 | 7 | 49 | 37 | 2b | 249 | 2 | 1a7 | 17ac63 | 158 | 13b65 | 1249 | 1 | 1 | 0d | 0c37 |
| 15 | 7 | 5 | 3b | 3 | 27 | 2 | 1d | 1a | 17 | 156c4 | 13b | 124936dca5b8 | 1 | 1 | 0e |
| 16 | 8 | 5 | 4 | 3 | 2a | 249 | 2 | 1c7 | 19 | 1745d | 15 | 13b | 1249 | 1 | 1 |
| 17 | 8 | 5b | 4 | 36da | 2e | 274e9c | 2 | 1f | 1bf5 | 194adf7c63 | 17 | 153fbd | 13afd6 | 1249 | 1 |
| 18 | 9 | 6 | 49 | 3ae7 | 3 | 2a5 | 249 | 2 | 1e73a | 1b834g69ed | 19 | 16gb | 152a | 13ae7 | 1249 |
| 19 | 9 | 6 | 4e | 3f | 3 | 2dag58 | 27 | 2 | 1h | 1dfa6h538c | 1b | 18ebd2ha475g | 16ehc4 | 15 | 13ad |
| 20 | a | 6d | 5 | 4 | 36d | 2h | 2a | 248hfb | 2 | 1g759 | 1d6 | 1af7dgi94c63 | 18b | 16d | 15 |
| 21 | a | 7 | 5 | 4 | 3a | 3 | 2d | 27 | 2 | 1j |
1f | 1cj8 | 1a | 18 | 16bh |
| 22 | b | 7 | 5b | 48hd | 3e | 3 | 2gb | 29h | 248hd | 2 | 1i7 | 1f5 | 1c | 1a5j | 185b |
| 23 | b | 7f | 5h | 4di9 | 3j | 36d | 2k | 2chka5 | 26kg | 2 | 1l | 1hfl57 | 1ei | 1c63 | 1a |
| 24 | c | 8 | 6 | 4j | 4 | 3a6kdh | 3 | 2g | 29e | 248haljf6d | 2 | 1k795cm3geib | 1h3a6kd | 1e9 | 1c |
| 25 | c | 8 | 6 | 5 | 4 | 3e7 | 3 | 2jb | 2c | 26kb9 | 2 | 1n | 1jg | 1g | 1e |
| 26 | d | 8h | 6d | 5 | 48h | 3iem7b | 36d | 2n | 2f | 29bl7 | 248h | 2 | 1m7b3ie | 1j | 1g6d |
| 27 | d | 9 | 6k | 5alg | 4d | 3n | 3a | 3 | 2io8 | 2c79m | 26k | 2 | 1p | 1lg5a | 1if5 |
| 28 | e | 9 | 7 | 5gmb | 4i | 4 | 3e | 3 | 2mb5g | 2f7hmpcka5 | 29 | 248h6cpnjalf | 2 | 1o7d | 1l |
| 29 | e | 9j | 7 | 5n | 4o | 4 | 3i | 36cpmg | 2q | 2id57qafnl | 2c | 26k | 2 | 1r | 1ng9 |
| 30 | f | a | 7f | 6 | 5 | 48h | 3mf | 3a | 3 | 2logar85dj | 2f | 296rkn | 248h | 2 | 1q7f |
| ........... | ............ | ............... | ........... |
Divisibility test for alpha numbers and factors
The base-n divisibility test applying to a factor of alpha = (n + 1), involves taking the alternating sum. We add all the even-ordered and all the odd-ordered digits of an integer separately, then subtract one sum from the other. The alternating sum of 12345 is (1 + 3 + 5) − (2 + 4) = 9 − 6 = 3. The alternating sum is a practical divisibility test method so long as the number of digits to evaluate is reasonable.
Decimally the alpha test pertains to 11, where it is rather rarely used. We know, for example, that decimal 14762 is divisible by 11 since (1 + 7 + 2) − (4 + 6) = 10 − 10 = 0; 0 is a multiple of 11. (14762 = 114 + 11².)
In nonary (base 9) we would apply the alpha test for the number 5. The nonary number “1336” is divisible by 5 since “(1 + 3) − (3 + 6)” = “4 − 10” = “−5”, which is clearly a multiple of 5. (Nonary “1336” = decimal 1005.)
The alpha test is fairly common across many number bases n, especially those for which (n + 1) is relatively highly factorable or at least composite, with small primes as factors. It is especially useful in bases 11 and 14, for example. In base 10, the test is not very important as it pertains to the fifth prime; in the map we can see that ten represents a “dry spot” regarding alpha totatives and thus small inheritors.
Alpha inheritors
An alpha inheritor is a composite number k with at least two distinct prime factors p, with one of the prime power factors pm | k also divides (n + 1).
There are two kinds of alpha inheritors, necessarily composite numbers that have an alpha factor tα | (n + 1) as a divisor. The alpha-regular inheritor involves at least one factor r regular to n and sometimes a factor coprime to n in addition to tα, and is semicoprime to n. The alpha-coprime inheritor involves only factors t coprime to n in addition to tα.
We are mostly concerned with simple alpha-regular inheritors as the numbers to which they pertain are fairly small and handy.
A simple alpha regular inheritor (sα ■) is a necessarily composite sα= r × tα semicoprime to n such that the coprime factor tα divides (n + 1) and the regular factor r is practical. Armed with a regular divisibility test for r and an alpha divisibility test for tα, we can use a compound divisibility test for the alpha inheritor sα. In base 14, given the test for 5 and the tetradecimal evenness test, we can determine whether an arbitrary tetradecimal number x is divisible by ten. Example: the above-mentioned tetradecimal number “516” is known to be divisible by five since (5 + 6) − 1 = ten which is clearly divisible by five. We know it is also divisible by ten since it ends in one of {0, 2, 4, 6, 8, a, c}, where “a” = digit ten and “c” = digit twelve. This is akin to the decimal divisibility test for 6; we know if a number is divisible by three and is even, it is divisible also by 6. In base fourteen there are plenty of alpha inheritors; 6, 12, and 21 inherit from tα= 3, and 10, 20, and 35 inherit from 5, to name a few. In octal, we have 6, 12, 18, and 24 inheriting from tα= 3.
Simple alpha coprime inheritors are necessarily composite products of an alpha factor tα and a number t coprime to n for which we have a workable divisibility test. All of the prime power factors of an alpha coprime inheritor either divide (n + 1), or are alpha-2 or omega-2 factors. In octal, we have a compound divisibility test for “17” (fifteen) via the alpha test for 3 and the alpha-2 test for 5. For octal, it is anticipated that the alpha-2 test for 5 would constitute a fairly handy “Rule of 5” divisibility test, not quite as eminent as the decimal Rule of 3, but more handy than the non-intuitive decimal divisibility test for 7 is today. Since the octal “Rule of 5” might prove fairly handy, we would see a compound rule combining the test for 3 and that for 5 to determine numbers divisible by 15, though this would seem to be far less necessary than the decimal divisibility rule approach to testing for divisibility by 6.
The number k = 15 = 3 × 5 is a compound alpha-coprime inheritor in bases 2, 8, 17, 23, etc.; any base n mod k ≡ 2 or 8. In these bases, we combine the alpha test for 3 and the alpha-2 test for 5 to arrive at a compound test for 15. The number k = 39 = 3 × 13 is a compound alpha-coprime inheritor in bases 5, 8, 44, 47, etc.; any base n mod k ≡ 5 or 8. We might anticipate that divisibility tests for large numbers may take a back seat to simply using division at some point.
The compound alpha-regular inheritor is any sω = r × tα × t semicoprime to n, where t is coprime to n and is a number for which we have a workable divisibility test. The number k = 60 = 2² × 3 × 5 is a compound omega-regular inheritor in base 2, 38, 62, 98, etc.; any base n mod k ≡ 2 or 38. In these bases, we combine the alpha test for 3, the regular test for 4, and the alpha-2 test for 5.
The map below plots alpha factors in green (tα ■) and simple alpha-regular inheritors in yellow-green (sα ■). Number base n appears on the vertical axis and digit k appears on the horizontal.
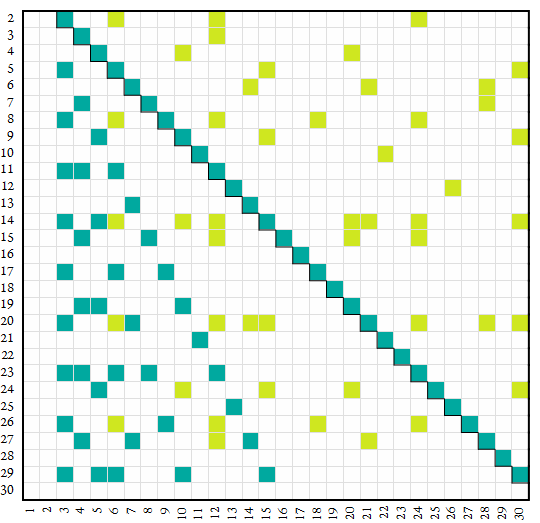
The alpha inheritors as denominators expanded in base n
Alpha inheritors sα in denominators of fractions 1/sα have mixed recurrent expansions in base k that feature at least one nonrepeating digit and two repeating digits. The number of nonrepeating digits varies as to the richness ε of the regular factor r of sα, i.e., there are ε nonrepeating digits. For example, in base 14, one twelfth = .12494949…, there are 2 nonrepeating digits and 2 repeating digits because 12 = r × tα = 4 × 3, 4 | 14² and 3 | (14 + 1).
The table below diagrams the behavior of numbers k at the top as unit fractions 1/k, with bold numerals nonrepeating, italic repeating. The alpha numbers and their factors tα > 2 appear in this version of the chart appear green (■), while the alpha inheritors appear in yellow-green (■). We also show the alpha-2-alpha inheritors in beige (■). This last variant has a purely recurrent period of 4.
Examples: we observe that in base 8, 1/6 = .1252525…, in base 9, 1/15 = .0535353…, and in base 14, 1/6 = .1494949…. If we move up to the next base (n + 1), the fractions are still mixed-recurrent; in base 8 + 1, 1/6 = .1444…, in base 9 + 1, 1/15 = .0666…, and in base 14 + 1, 1/6 = .2777….
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 2 | 1 | 01 | 01 | 0011 | 001 | 001 | 001 | 000111 | 00011 | 0001011101 | 0001 | 000100111011 | 0001 | 0001 | 0001 |
| 3 | 1 | 1 | 02 | 0121 | 01 | 010212 | 01 | 01 | 0022 | 00211 | 002 | 002 | 001221 | 00121 | 0012 |
| 4 | 2 | 1 | 1 | 03 | 02 | 021 | 02 | 013 | 012 | 01131 | 01 | 010323 | 0102 | 01 | 01 |
| 5 | 2 | 13 | 1 | 1 | 04 | 032412 | 03 | 023421 | 02 | 02114 | 02 | 0143 | 013431 | 013 | 0124 |
| 6 | 3 | 2 | 13 | 1 | 1 | 05 | 043 | 04 | 03 | 0313452421 | 03 | 024340531215 | 023 | 02 | 0213 |
| 7 | 3 | 2 | 15 | 1254 | 1 | 1 | 06 | 053 | 0462 | 0431162355 | 04 | 035245631421 | 03 | 0316 | 03 |
| 8 | 4 | 25 | 2 | 1463 | 125 | 1 | 1 | 07 | 06314 | 0564272135 | 052 | 0473 | 04 | 0421 | 02 |
| 9 | 4 | 3 | 4 | 17 | 14 | 125 | 1 | 1 | 08 | 07324 | 06 | 062 | 057 | 053 | 05 |
| 10 | 5 | 3 | 25 | 2 | 16 | 142857 | 125 | 1 | 1 | 09 | 083 | 076923 | 0714285 | 06 | 0625 |
| 11 | 5 | 37 | 28 | 2 | 19 | 163 | 14 | 124986 | 1 | 1 | 0a | 093425a17685 | 087 | 08 | 0762 |
| 12 | 6 | 4 | 3 | 2497 | 2 | 186a35 | 16 | 14 | 12497 | 1 | 1 | 0b | 0a35186 | 09724 | 09 |
| 13 | 6 | 4 | 3 | 27a5 | 2 | 1b | 18 | 15a | 13b9 | 12495ba837 | 1 | 1 | 0c | 0b36 | 0a74 |
| 14 | 7 | 49 | 37 | 2b | 249 | 2 | 1a7 | 17ac63 | 158 | 13b65 | 1249 | 1 | 1 | 0d | 0c37 |
| 15 | 7 | 5 | 3b | 3 | 27 | 2 | 1d | 1a | 17 | 156c4 | 13b | 124936dca5b8 | 1 | 1 | 0e |
| 16 | 8 | 5 | 4 | 3 | 2a | 249 | 2 | 1c7 | 19 | 1745d | 15 | 13b | 1249 | 1 | 1 |
| 17 | 8 | 5b | 4 | 36da | 2e | 274e9c | 2 | 1f | 1bf5 | 194adf7c63 | 17 | 153fbd | 13afd6 | 1249 | 1 |
| 18 | 9 | 6 | 49 | 3ae7 | 3 | 2a5 | 249 | 2 | 1e73a | 1b834g69ed | 19 | 16gb | 152a | 13ae7 | 1249 |
| 19 | 9 | 6 | 4e | 3f | 3 | 2dag58 | 27 | 2 | 1h | 1dfa6h538c | 1b | 18ebd2ha475g | 16ehc4 | 15 | 13ad |
| 20 | a | 6d | 5 | 4 | 36d | 2h | 2a | 248hfb | 2 | 1g759 | 1d6 | 1af7dgi94c63 | 18b | 16d | 15 |
| 21 | a | 7 | 5 | 4 | 3a | 3 | 2d | 27 | 2 | 1j |
1f | 1cj8 | 1a | 18 | 16bh |
| 22 | b | 7 | 5b | 48hd | 3e | 3 | 2gb | 29h | 248hd | 2 | 1i7 | 1f5 | 1c | 1a5j | 185b |
| 23 | b | 7f | 5h | 4di9 | 3j | 36d | 2k | 2chka5 | 26kg | 2 | 1l | 1hfl57 | 1ei | 1c63 | 1a |
| 24 | c | 8 | 6 | 4j | 4 | 3a6kdh | 3 | 2g | 29e | 248haljf6d | 2 | 1k795cm3geib | 1h3a6kd | 1e9 | 1c |
| 25 | c | 8 | 6 | 5 | 4 | 3e7 | 3 | 2jb | 2c | 26kb9 | 2 | 1n | 1jg | 1g | 1e |
| 26 | d | 8h | 6d | 5 | 48h | 3iem7b | 36d | 2n | 2f | 29bl7 | 248h | 2 | 1m7b3ie | 1j | 1g6d |
| 27 | d | 9 | 6k | 5alg | 4d | 3n | 3a | 3 | 2io8 | 2c79m | 26k | 2 | 1p | 1lg5a | 1if5 |
| 28 | e | 9 | 7 | 5gmb | 4i | 4 | 3e | 3 | 2mb5g | 2f7hmpcka5 | 29 | 248h6cpnjalf | 2 | 1o7d | 1l |
| 29 | e | 9j | 7 | 5n | 4o | 4 | 3i | 36cpmg | 2q | 2id57qafnl | 2c | 26k | 2 | 1r | 1ng9 |
| 30 | f | a | 7f | 6 | 5 | 48h | 3mf | 3a | 3 | 2logar85dj | 2f | 296rkn | 248h | 2 | 1q7f |
| ........... | ............ | ............... | ........... |
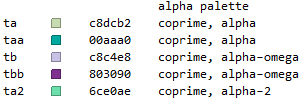
Color Canon
The colors used to represent alpha numbers and factors in this work appear in the table below:
References
Michael De Vlieger, Exploring Number Bases as Tools, ACM Inroads, 2012, Vol. 3, No. 1, 4-12.
Marc Renault, Stupid Divisibility Tricks, (See PDF), Section 3.3, Math Horizons (2006). Retrieved in June 2019.
Maths Is Fun, Divisibility Rules, see “11” and “Factors Can Be Useful”. Retrieved in June 2019.
Hardy & Wright 2008, Chapter IX, “The Representation of Numbers by Decimals”, Section 9.6, “Tests for divisibility”, page 147, specifically: “Since 10 ≡ −1 (mod 11), we have 102r ≡ 1, 102r + 1 ≡ −1 (mod 11), so that A1.10s + A2.10(s − 1) + … + As.10 + A(s + 1) ≡A(s + 1)− As + A(s − 1) … (mod 11). A number is divisible by 11 if and only if the difference between the sums of its digits of odd and even ranks is divisible by 11.”